L’ascensore gravitazionale
L’ASCENSORE GRAVITAZIONALE
…ovvero: come muoversi in 42 minuti per qualsiasi direzione sulla Terra.
Sì, ma… con qualche trucco!
La teoria

In questi giorni sui principali social forum sta circolando l’immagine a lato. “Oh… ma perdindirindina… ma… allora… gli aeroplani e i lunghi viaggi intercontinentali in futuro spariranno!”
Questo è ciò che la persona comune potrebbe pensare leggendo questo post circolante sui social forum e condiviso da persone che, presumibilmente a corto di nozioni al riguardo, non si sono nemmeno poste la domanda più banale:
Se un paracadutista in caduta libera precipita a 200 km/h, com’è possibile con la sola forza di gravità viaggiare a 18.000 km/h ?
In effetti il diametro della terra è circa 12.700 Km che diviso per 42/60 da circa 18.180 km/h.
La risposta che la mia mente ha partorito è che oggi, nell’anno 2016, in presenza di aria, è fisicamente impossibile senza una forza esterna. Anzi, a onor del vero, una tale opera sarebbe impossibile per ben più di una ragione:
- Il nucleo terrestre ha una temperatura compresa tra i 3.000°C e i 5.000°C circa. Ammesso che qualcuno volesse farlo, questo viaggio non sarebbe proprio un’impresa facile facile.
- Detto nucleo ha pressioni variabili sull’ordine di milioni di bar (1.500-3.000 Kbar), intollerabili per le tecnologie esistenti oggi. Come riferimento a titolo di paragone, citiamo la pressione atmosferica terrestre che è +/- 1 bar mentre sul fondo della Fossa delle Marianne, la massima profondità marina posta a circa -11.000 m la pressione dell’acqua è +/- 1.100 bar (1,1 Kbar) ovvero 1.100 kg su ogni cm². Ecco, ora immaginate che nel nucleo terrestre tutto questo sia moltiplicato per 1.500-3.000 volte. Un bel problemino, vero?
- Infine, dopo tutto ciò, permangono chiari problemi tecnici sulla fattibilità di un tunnel lungo centinaia, migliaia o una decina di migliaia di km.
Tuttavia ignoreremo questi ostacoli, perchè ci interessa analizzare l’argomento sotto l’aspetto prettamente fisico-teorico e non di fattibilità tecnica poiché per questo abbiamo già una facile risposta.
Corda e diametro.
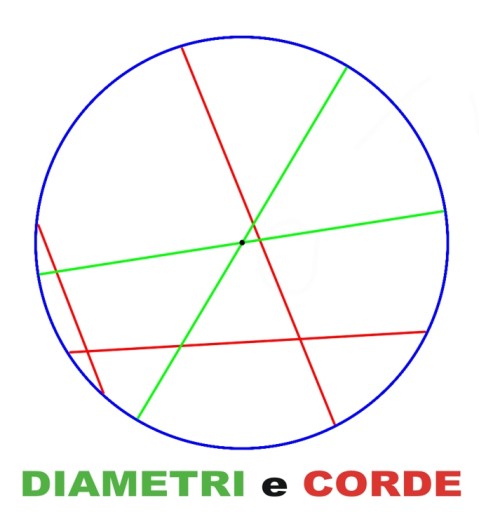
La teoria sostiene che il viaggio nel tunnel non dipenda dalla sua lunghezza, giacché non è detto che esso sia necessariamente un diametro terrestre, ma potrebbe anche essere una corda.
Ma com’è possibile che il viaggio duri un tempo fisso a prescindere dalla distanza percorsa? Cioè: perché su lunghe distanze si viaggia veloci e su quelle corte si viaggia a rilento?
Premettiamo subito che una condizione indispensabile perché ciò si verifichi (e posto ovviamente in essere gli ostacoli citati) è che ci dobbiamo trovare in totale assenza di attriti, quindi essere nel vuoto.
Questo fa la differenza: l’aria (o altro fluido) infatti crea un attrito che rende fisicamente impossibile questo concetto. Ma nell’ipotesi che una sfortunata cavia decida di fare il viaggio in un tunnel sotto vuoto e ipotizzando che il tunnel sia opportunamente attrezzato per questo, vediamo cosa accadrebbe, analizzando due esempi: un viaggio in un tunnel-diametro (che passa quindi per il centro del pianeta) e un viaggio più breve (come distanza) che sarebbe un tunnel-corda. Presupponiamo infine che la Terra sia una sfera perfetta e di densità omogenea.
Prima però introduciamo un concetto legato alla forza peso (Fp) e alla forza gravità (g) grazie alle quali tutti siamo attratti dalla Terra. Quando una persona è ferma sul suolo, la gravità g si manifesta solo sulla Fp (in pratica quello che sentite sulle vostre gambe quando siete in piedi) e la vostra bilancia ve lo può confermare. Ma un paracadutista o un tuffatore, nel momento di caduta libera “pesano” zero perchè g si trasforma in accelerazione (Fa) responsabile della velocità di caduta. Una volta al suolo, Fa ritorna = 0 e Fp ritorna = g ridando gravità alla persona ferma al suolo. In realtà l’aria “frena” il paracadutista non permettendogli di superare 200-250 km/h e questo si trasforma in una piccola forza di gravità. Se ci fosse il vuoto in caduta, questa forza sarebbe = 0.
Tunnel diametro
Immaginate un pozzo privo di aria e perfettamente a 90° rispetto al terreno dove la nostra temeraria cavia si appresta a lanciarsi di piedi sapendo che dovrà percorrerlo senza mai toccare le pareti per non creare attrito. Quando parte, subito la forza gravitazionale terrestre se lo accalappia: g=Fa (la forza di gravità si trasforma tutta in accelerazione) e Fp= 0 (lui si sente “senza gravità”, cioè senza forza peso, come il tuffatore in volo). L’accelerazione di partenza è 9.8 m/sec².
Per ogni secondo che passa, la velocità della cavia aumenta di circa 35,3 km/h ovvero, dopo 1 minuto viaggerà a a oltre 2.100 km/h. Ciò avviene in quanto la massa terrestre responsabile della gravità è temporaneamente tutta sotto i suoi piedi, come avviene per qualsiasi essere che cammina sulla Terra.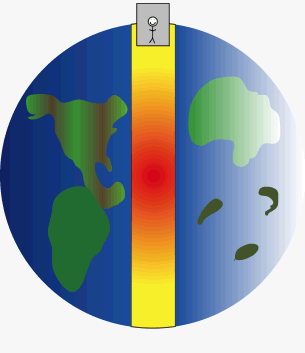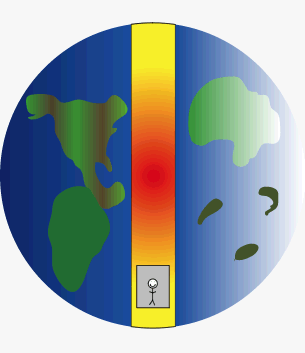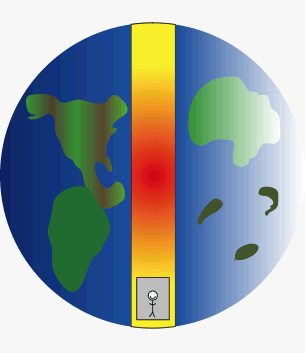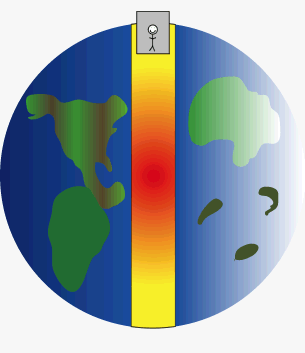
Ma durante il viaggio egli avrà progressivamente sempre più massa terrestre sulla sua testa e sempre meno massa sotto i piedi, per cui già dalla partenza la sua accelerazione di 9.8 m/sec² non sarà costante ma andrà progressivamente a calare fino a raggiungere lo zero al centro della terra.
Al centro della Terra si troverà in totale assenza di forze di campo gravitazionale perché esse sono tutte in egual misura attorno a lui, a 360° sui 3 assi spaziali. L’animazione a lato rende bene in concetto con i colori che da giallo (g) diventa via via rosso (zero g) per poi tornare come in origine. Se la cavia si fermasse qui, galleggerebbe immobile nel vuoto, priva di ogni forza come un astronauta che galleggia nel vuoto lontano da ogni corpo celeste..
Ma il viaggio continua: mentre si raggiunge la velocità massima che diventa temporaneamente stabile egli procederà solo per inerzia cinetica. Naturalmente solo per un istante.
Passato il centro della Terra infatti, la massa sopra la testa sarà via via sempre maggiore rispetto a quella sotto i piedi: questo causerà un’accelerazione negativa (decelerazione) al pari di quella avuta nella prima metà del viaggio e la velocità, nella stessa misura in cui è aumentata, diminuisca fino ad arrivare a zero all’uscita del tunnel: lì il nostro amico coraggioso si troverà agli antipodi in poco più di 42 minuti, e se ha scelto il tunnel-diametro giusto sarà passato dall’estate all’inverno o viceversa.
Se non fosse lesto nell’uscirne, però, verrebbe ri-accalappiato dentro per ripetere la stessa dinamica, e poi ancora, ancora, all’infinito, in un moto oscillatorio perpetuo, possibile solo in assenza di attriti: un cambio di stagione quindi ogni 42 minuti.
Tunnel corda
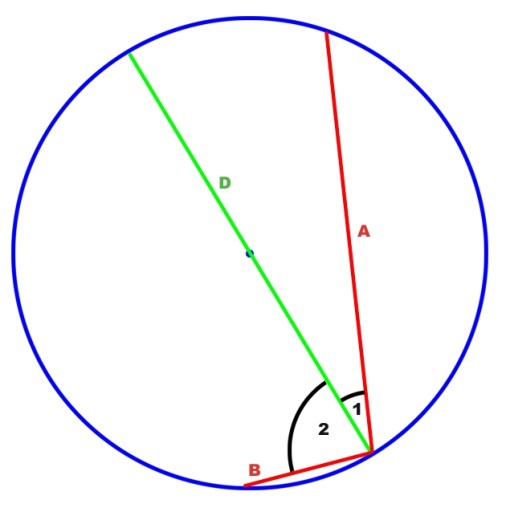
Ora immaginate un pozzo che non sia perfettamente verticale ma inclinato. Volgarmente un pozzo “storto”. Se continuasse in linea retta raggiungerebbe l’altra parte della Terra senza passare per il centro: una corda appunto. Ai vostri occhi potrebbe apparire come un tunnel-pozzo “quasi verticale” (cioè una corda abbastanza lunga come la A nel disegno sotto) oppure un tunnel in discesa come la corda B sempre nella stessa immagine.
Quanto detto fino ad ora per un tunnel-diametro, cioè un pozzo a 90°, un pozzo “dritto”, sostanzialmente vale anche per un tunnel che non passi per il centro della terra, un tunnel-corda, volgarmente inclinato. Ma c’è una grande differenza: il centro della terra, che corrisponde al centro della massa terrestre, durante la prima parte del viaggio non è verticalmente sotto ai piedi del viaggiatore in quanto la corda non transita per il centro della Terra e questo è causa di una forza Fp che per il viaggiatore sarà recepita come gravità. Lo potete facilmente capire se vi buttate dentro un pozzo storto o più o meno inclinato: andreste a sbattere da un lato, che chiamereste “il basso” perché, se il pozzo fosse “molto storto” potreste anche camminarvici sopra come una rampa sotterranea.
Cosa significa tutto questo? Che forza di gravità g (che come abbiamo visto varia a seconda della distanza dal centro della Terra) viene scomposta in 2 componenti: Fa che è la forza utile ad accelerare la cavia e Fp che è la rimanente e che di fatto ci dà gravità: la forza peso.La somma di queste due forze Fa+Fp=g
Quindi:
- Già alla partenza Fa sarà minore di g e quindi ci sarà una rimanente componente Fp che darà un po’ di gravità verso la parete del tunnel che è rivolta in direzione del centro della Terra e che per il viaggiatore sarà il “pavimento”.
- Per tutto il viaggio egli si dovrà difendere da questa forza Fp con intensità e verso variabile a seconda della lunghezza del tunnel-corda e del punto in cui il viaggiatore si trova.
- A metà percorso, dove anche qua come prima Fa = 0 e la velocità è massima (quindi un moto solamente inerziale), il viaggiatore permarrà in
 presenza di forza Fp ortogonale al “pavimento”.
presenza di forza Fp ortogonale al “pavimento”. - Poi ritorna Fa con verso contrario che farà rallentare la cavia fino a velocità zero all’ìuscita. E anche qui se egli non uscirà sarà risucchiato dentro in un altro moto oscillatorio perpetuo come il precedente.
- Tuttavia la differenza più importante è relativa alla nostra corda. Guardando il disegno a lato notiamo che gli angoli 1 e 2 cambiano a seconda della lunghezza della corda (A e B). Espressamente la forza responsabile della accelerazione cioè Fa lungo la corda sarà solo una parte della forza g a disposizione. Nel tunnel-diametro (D) questo angolo è 0 quindi si può sfruttare tutta la forza g, ovvero Fa=g ma in una corda, via via che questo angolo aumenta (1 e poi 2), Fa sarà sempre minore mentre sarà sempre maggiore Fp che conferirà gravità al viaggiatore. Più precisamente Fa dipende dal coseno dell’angolo in questione infatti nel tunnel-diametro dove l’angolo = 0 il cos = 1 (quindi abbiamo il 100% di g sfruttabile ovvero Fa=g ). In una corda dove l’angolo è ad esempio di 60° avremo solo il 50% disponibile (cos 60 = 0.5 ergo Fa=Fp) mentre un angolo di 90° (che equivale ad un tunnel lungo zero) la forza sfruttabile per accelerare è zero ovvero Fa=0 perchè questa va tutta in gravità cioè Fp=g che è poi quello che ci capita tutti i giorni quando stiamo in piedi.
- Se il nostro tunnel fosse relativamente breve, da poter garantire sufficiente gravità Fp atta a camminare, avreste la strana sensazione di camminare in discesa all’inizio, per poi via via andare pari e infine risalire sempre più progressivamente, esattamente al contrario dell’andata. Come se aveste percorso un grande e profondo sottovia. Ma il tunnel è rettilineo! Dove sta l’arcano? Sta nel fatto che sì, il tunnel è rettilineo, ma sono gli effetti della gravità a cambiare e a darvi l’impressione di essere in salita o in discesa. E in un certo senso è vero: prima andate verso la massima profondità e poi ritornate in superficie. Il tutto il modo rettilineo e se rileggete questo passaggio osservando la corda A del disegno sopra e tenendo presente una componente Fp sempre e comunque rivolta verso il centro della terra, capirete in maniera semplice che l’accelerazione in discesa e la decelerazione in salita corrispondevano ad una forza Fa che va via via a zero fino a metà percorso (il “piano”) e ritorna uguale e contraria nella seconda metà del percorso dandovi la salita.

Volendo spiegarci ancora meglio, poniamo 3 esempi di una persona che cammina: in figura A1 immaginate di percorrere un normale sottopassaggio: date le sue corte dimensioni a confronto della Terra, le linee di forza gravitazionali rappresentate dalle frecce sotto si possono considerare uguali e parallele tra loro in tutto il percorso: quindi percepirete prima la discesa, poi il pari e infine la salita come ad occhio è. Anche lo schema B1 è intuibile: sulla superficie della Terra si cammina sempre coi piedi rivolti al centro. Ma in una corda (in rosso) se la gravità Fp ce lo permette, come si cammina? In C1 dove il centro di gravità è il puntino sotto (e dove la forza di gravità è inversamente proporzionale alla lunghezza delle linee grige) all’inizio avrete una spinta che percepirete come discesa g=Fa+Fp, a metà avrete solo una gravità g=Fp (Fa=0) che vi darà l’impressione di camminare in piano e alla fine la salita reciproca della discesa iniziale con gli stessi valori di forze in gioco ma con Fa di verso contrario. Il tutto in un moto perfettamente rettilineo.
In definitiva più la corda è breve e minore sarà la nostra velocità massima perché minore è Fa, mentre la rimanente, ovvero tutto ciò che non viene usato per accelerare, cioè Fp, ci da gravità.
Calcoli alla mano, la lunghezza del tunnel e proporzionale alla velocità media quindi il rapporto (ovvero il tempo impiegato) è costante: poco più di 42 minuti sempre e comunque (sulla Terra). Questo tempo potrebbe variare su un altro corpo celeste di diversa densità. Tra l’altro in luoghi come la Luna senza atmosfera, l’idea avrebbe un ostacolo in meno perché il vuoto risolverebbe uno dei tanti problemi.
Agli effetti pratici però…
Escludendo i limiti tecnici di costruzione del tunnel, e anche quelli già citati imputabili a pressione e temperatura del nucleo terrestre, c’è un ostacolo causato dall’aria.
Se nel vuoto assoluto (e in assenza di altri attriti) un corpo può raggiungere teoricamente qualsiasi velocità, in presenza di aria la cosa cambia completamente in quanto dobbiamo fare i conti con gli attriti.
Una paracadutista in caduta libera che si lancia da 3000-4000 m di quota, causa l’attrito con l’atmosfera, non può superare una velocità massima di 200 – 250 km/h (a seconda della posizione più o meno aerodinamica adottata). Se si lanciasse da molto più in alto avrebbe una velocità ben maggiore perché l’aria è meno densa.
Pertanto il nostro amico viaggiatore che si lanciasse di piedi nel nostro tunnel-diametro con aria, non oltrepasserebbe una velocità di 250-300 km/h. Ma a questa velocità basterebbero pochi km per fermarsi nel centro della terra in quanto lì terminerebbe il carburante cioè Fa=g=0, facendo rimanere intrappolata, ferma e galleggiante la nostra povera cavia.
Nel tunnel-corda accadrebbe la stessa cosa con la differenza che permane una Fp cioè una gravità, a scapito di una minor Fa. Se il tunnel è relativamente corto, Fp potrebbe permettere al nostro amico cavia un sufficiente attrito verso la parete pavimento tale da camminarci e riuscire a salvarsi. Come nello schema C1 visto prima.
Tutto ciò è una ulteriore prova dell’impossibilità del moto perpetuo, infatti nella discesa l’energia potenziale del viaggiatore si trasforma in energia cinetica che lo fa arrivare fino al centro della Terra. E basta! Se potesse pendolare all’infinito, chi gli fornirebbe l’energia cinetica necessaria?
Che brutto mestiere quello della cavia scientifica… Sconsiglio vivamente di farlo.
Ancor più concretamente
Un tunnel ferroviario/autostradale in perfetto piano si può ragionevolmente considerare una corda come nel nostro esempio, con la basilare caratteristica che, essendo brevissimo (in proporzione alla circonferenza terrestre) la forza di gravità Fp sarebbe praticamente = g mentre quella che darebbe accelerazione Fa nel tunnel sarebbe di fatto zero. Ma analiticamente non è così e lo possiamo provare con un banale esempio: i 52 km del tunnel del San Gottardo. Naturalmente, per soli fini di ragionamento, non teniamo conto delle irregolarità delle masse delle montagne che in un tunnel-corda così breve potrebbero interferire nei calcoli.
Pensiamo dunque solamente ad un tunnel-corda di 52 km a fronte di un raggio terrestre di 6.350 km. Con riferimento al secondo disegno sopra, l’angolo 2 sarà pari a 89.872° per cui solo una minimissima componente di g sarebbe Fa sfruttabile per il nostro viaggio gravitazionale in assenza totale di attriti, ovvero lo 0.0022 % , mentre prevarrebbe di gran lunga Fp l’effetto gravità, che al km 27, a metà percorso, il più vicino al centro della Terra, equivarrebbe al restante 99,9978% di g. Cioè a metà di questo tunnel un uomo di 80 kg “peserebbe” solo 2 grammi in meno.
E difatti da un tunnel del genere è possibile uscirne camminando. Quando si dice la… precisione svizzera…
Un tunnel gravitazionale di 54 km non sarebbe molto vantaggioso perchè Fa è quasi zero e tutta la forza g potenzialmente utile se ne va in gravità Fp facendoci comunque sempre impiegare 42 minuti, ma a fronte di una velocità media di 77 km/h.
Prendiamo il treno che è meglio!
Conclusioni
Con una certa approssimazione di linguaggio, si può ragionevolmente sostenere che nel vuoto il tempo è costante perché al diminuire della lunghezza del tunnel, diminuisce proporzionalmente la velocità media dovuta ad un minor Fa che è lo “sfruttamento” di g.
In un altro modo, più filosofico se vogliamo, si può sostenere che la forza gravitazionale è lì disponibile a chiunque: scegli tu come utilizzarla e quanto utilizzarne facendo un tunnel più o meno lungo dove quello che non utilizzi per viaggiare (Fa) la consumi per stare +/- attratto dal pavimento (Fp). Più la corda è lunga e più utilizzi Fa fino al tunnel-diametro dove l’utilizzo di Fa è del 100%. E viceversa.
Perché il post attribuito a National Geographic abbia però validità, serve un tunnel nel vuoto: in tal caso l’ascensore gravitazionale funzionerebbe. Con l’aria rimarremmo prigionieri al centro della Terra senza energia per la risalita.
Va precisato che non è stato il National Geographic a ipotizzare per primo questa teoria, perché essa è molto più vecchia di quanto voi possiate immaginare: nel XVII secolo, lo scienziato britannico Robert Hooke in una lettera a Isaac Newton espose l’idea dell’accelerazione di un oggetto all’interno del globo terrestre. Un progetto fu poi realmente presentato all’Accademia delle Scienze di Parigi nel XIX secolo. Infine l’idea fu rispolverata negli anni sessanta. (Da Wikipedia)
Eh si, a quanto pare i cervelloni esistevano anche una volta quando non c’erano i computer, in barba alle orde di giovani complottisti che credono che in passato tutti fossero stupidi e che nulla fosse possibile senza l’aiuto degli alieni.
Chissà se le migliaia di persone che hanno condiviso questo post sui social forum sanno tutto ciò?
Dedichiamo dunque questo articolo a questi eventuali fruitori del web nella speranza che la moda del condividi-e-getta lasci posto al condividi-rifletti-e-approfondisci.
Ci credete voi?
Se ci credete ci credo anch’io…
Lola Fox
Se ti è piaciuto l’articolo, sostienici su Patreon! Può bastare anche il costo di un caffè!








